LCS Algorithm
마이구미의 HelloWorld, 마이구미 님의 블로그를 참고하여 정리했습니다.
1. (Longest Common) Substring과 Subsequence의 차이
- (최장 공통 부분) 문자열: 전체 문자열 중에서 공통되는 부분 문자열중 길이가 가장 긴 것
- (최장 공통 부분) 수열: 전체 문자열 중에서 공통되는 부분 문자열들의 세트
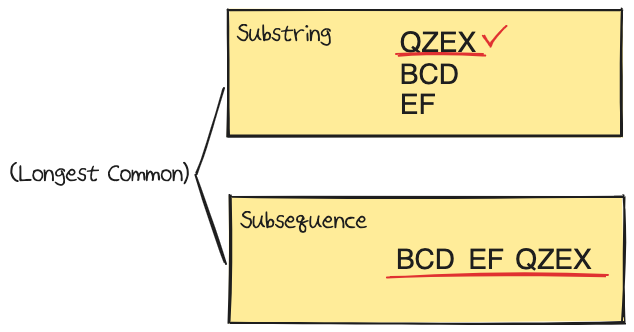
두 문자열 'ABCDHEFQZEX'와 'UBCDEFLQZEXKK'를 가지고 LCSubstring과 LCSubsequence를 구해보자. 우선 각 문자열의 공통 문자열을 체크하면 다음과 같다.

이렇게 되었을 때, LCSubstring은 'QZEX' (문자열 길이가 4로 제일 김), LCSubsequence는 'BCDEFQZEX'가 된다.
2. 수식
두 LCS는 수식으로 볼 때 이해가 가장 빠른 것 같다. 최장 공통 부분 문자열을 찾아내기 위한 알고리즘의 수식은 다음과 같다. 2차원 배열에 문자열의 문자가 하나씩 나열되어 있고, 그 안의 값은 최대 문자열의 문자수 혹은 수열의 문자 개수라고 생각하자 (0은 문자가 없는 것을 의미하며 인덱스0 행과 0열은 모두 0으로 채워진다.)
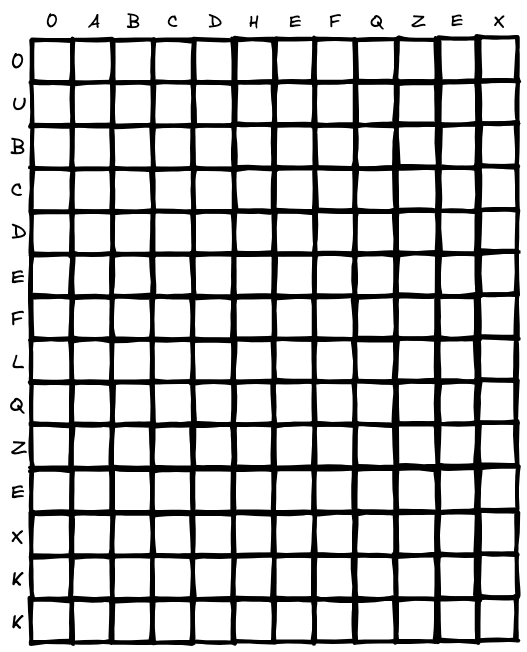
2-1. LCS - Longest Common Substring (최장 공통 부분 문자열)
문자열 S와 문자열 T를 가지고 할 때,
[p]행의 문자와 [q]열의 문자가
- 같으면,
[p][q]에[p-1][q-1]값에 1을 더한 값을 넣는다.
(= 직전에 공통 문자열에 문자를 하나 더 추가할 수 있는 경우이다.). - 다르면, 공통 문자열이 이 부분에서 끝나게 되는 것이므로
[p][q]에 0을 넣는다.
2-2. LCS - Longest Common Subsequence (최장 공통 부분 수열)
[p]행의 문자와 [q]열의 문자가
- 같으면,
[p][q]에[p-1][q-1]값에 1을 더한 값을 넣는다.
(= 직전에 공통 문자열에 문자를 하나 더 추가할 수 있는 경우이다.). - 다르면, 위의 행와 왼쪽의 열 중에서 큰 값을 넣는다.
(= 위의 행과 왼쪽 열은 그곳까지 탐색해 온 공통 부분 문자열들의 총 길이를 나타낸다.)
3. 구현
3-1. 알고리즘
public class LCS {
static int findLCSubstring(String s, String t) {
int[][] LCS = new int[s.length() + 1][t.length() + 1];
int maxLength = 0;
for (int i = 1; i <= s.length(); i++) {
for (int j = 1; j <= t.length(); j++) {
if (s.charAt(i - 1) == t.charAt(j - 1)) {
LCS[i][j] = LCS[i - 1][j - 1] + 1;
if (maxLength < LCS[i][j]) {
maxLength = LCS[i][j];
}
}
}
}
return maxLength;
}
static int findLCSubsequence(String s, String t) {
int[][] LCS = new int[s.length() + 1][t.length() + 1];
for (int i = 1; i <= s.length(); i++) {
for (int j = 1; j <= t.length(); j++) {
if (s.charAt(i - 1) == t.charAt(j - 1)) {
LCS[i][j] = LCS[i - 1][j - 1] + 1;
} else {
LCS[i][j] = Math.max(LCS[i - 1][j], LCS[i][j-1]);
}
}
}
return LCS[s.length()][t.length()];
}
}
3-2. 테스트
public class LCSTest {
public static void main(String[] args) {
LCS lcs = new LCS();
String s = "ABCDHEFQZEX";
String t = "UBCDEFLQZEXKK";
int lcsSubstring = lcs.findLCSubstring(s, t);
int lcsSubsequence = lcs.findLCSubsequence(s, t);
System.out.println("lcsSubstring=" + lcsSubstring + ", lcsSubsequence=" + lcsSubsequence); // lcsSubstring=4, lcsSubsequence=9
}
}